
Computervidenskab
En computer kan tage mange former. Lige fra en almindelig laptop eller telefon til et ur eller et køleskab. Der er computere i mange ting, og ofte tager vi det for givet, at vores devices fungerer og kan tale sammen. Vi har set på internettets arkitektur og kommunikation mellem computere. Nu skal vi se nærmere på hvordan en computer fungerer og hvad en computer er.
Hvad er en computer
Der er fire funktioner, som skal være tilstede for at vi kan tale om en computer. en computer skal kunne:
- modtage et input (input)
- gemme denne information (storage)
- behandle denne information (processing)
- udlevere den behandlede information (output)
Hvad det helt præcist betyder, kan I se mere grundigt forklaret i videoen.
Binær data
Al information i computere bliver gemt og behandlet vha. elektroniske signaler i form af binære signaler. Det binære talsystem består af 0 og 1 (slukket eller tændt) og al data i en computer, lige fra tekst til lyd og billeder, er repræsenteret vha.det binære talsystem. Videoen forklarer mere præcist, hvordan dette sker.
Konvertering fra binære til decimal
For at kunne konvertere fra det binære talsystem (to-talssystemet) til decimaltalssystemet (ti-talssystemet 0-9), som vi bruger til dagligt, skal vi først se nærmere på decimaltalssystemets opbygning. Ved tallet 1345 er der 1×1000, 3×100, 4×10 og 5×1. Tallenes placering betyder altså noget for, hvilken værdi de har.
| 1000 | 100 | 10 | 1 |
| 1 | 3 | 4 | 5 |
I det binære talsystem er placeringen også afgørende for den samlede værdi. Så for at konvertere et tal fra to-talssystemet skal vi se på placeringen af de enkelte tal. Tallet 1345 vil i det binære talsystem blive 10101000001.
| 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
1024 + 0 + 256 + 0 + 64 + 0 + 0 + 0 +0 + 0 + 1= 1345
Øvelser i konvertering fra binære tal
Konverter disse binære tal til 10-talssystemet. Brug evt. nedenstående model til hjælp.
- 00000110
- 11000110
- 01100110
- 10010101
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Konverter disse 10-talssystemtal til det binær talsystem. Brug gerne nedenstående model til hjælp
- 17
- 130
- 110
- 87
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Kredsløb og logik
En computer bruger kredsløb til at behandle den binære data. Disse kredsløb kan tage forskellige funktioner, fx NOT-gates, AND-gates og OR-gates. En computer foretager simple operationer, som subtraktion og multiplikation, altså simple beregninger, som et menneske kan foretage. En computer gør det bare meget meget hurtigere.
Se videoen, der viser, hvordan kredsløb og logikken fungerer i en computer, og hvorfor en mindre computer er hurtigere.
Gates og boolske operatorer
Som vi så i videoen er der 3 grundlæggende gates; AND-gates, OR-gates og NOT-gates, som flipper signalet på hver sin måde. AND-gates og OR-gates får to signaler ind (A og B) og sender ét signal ud (Q). NOT-gates får ét signal ind (A)og sender ét signal videre (Q). Udgangssignalet Q er enten 1 eller 0 afhængig af indgangssignalerne og hvilken gate, der er tale om.
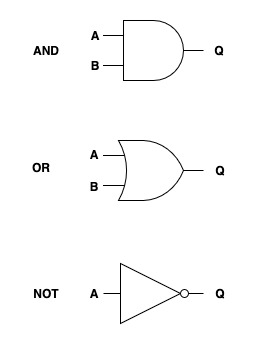
En AND-gate sender kun et signal, et 1-tal, hvis begge indgangsporte modtager et 1-tal. Hvis enten A eller B modtager et 0, bliver Q altid 0. En AND-gate bruger altså den boolske logik og/eller, som dikterer, at både A og (and) B skal være sand (1) for at output bliver sandt (1). Til venstre vises en sandhedstabel over mulige outputs i en AND-gate.
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
En OR-gate sender et signal, et 1-tal, hvis én af indgangsportene modtager et 1-tal. Hvis enten A eller B modtager et 1-tal, vil output altid være et 1-tal. Hvis A og B begge modtager et 0-tal, vil output være 0, men kun i det tilfælde. En OR-gate bruger altså den booleske logik enten eller/OR, som dikterer, at enten A eller B skal være sand (1) for at output bliver sandt (1). Til højre vises en sandhedstabel over mulige outputs i en OR-gate.
En NOT-gate adskiller sig fra de andre gates ved kun at tage ét input og giver også kun ét output. En NOT-gate flipper input fra 1 til 0, eller fra 0 til 1. Output er altså altid det modsatte af input. Den booleske logik i en NOT-gate dikterer, at input ikke skal være sandt (1), men altså falsk (0), for at være sandt (1). Til venstre vises en sandhedstabel over mulige outputs i en NOT-gate.
| A | Q |
| 0 | 1 |
| 1 | 0 |
Eksempel på sandhedstabel over diagram
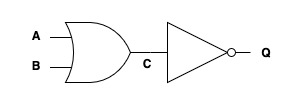
| A | B | C | Q |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
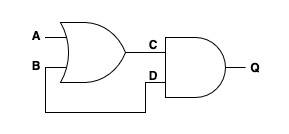
Øvelse i gates og boolsk logik 1
| A | B | C | D | Q |
| 0 | 0 | |||
| 0 | 1 | |||
| 1 | 0 | |||
| 1 | 1 |
Øvelse i gates og boolsk logik 2
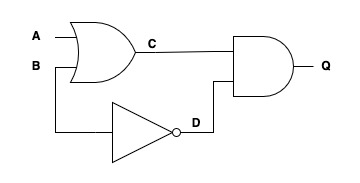
| A | B | C | D | Q |
| 0 | 0 | |||
| 0 | 1 | |||
| 1 | 0 | |||
| 1 | 1 |
Øvelse i gates og boolsk logik 3
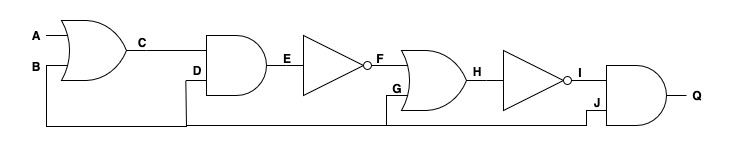
| A | B | C | D | E | F | G | H | I | J | Q |
| 0 | 0 | |||||||||
| 0 | 1 | |||||||||
| 1 | 0 | |||||||||
| 1 | 1 |